Genetic Method
The genetic method is a robust optimization algorithm that is designed to reliably locate a global optimum even in the presence of local optima. It is, however, quite slow. This algorithm should be considered when the Conjugate Directions and Variable Metric methods have failed and you are prepared to wait for calculations to reveal the true optimum point. Alternatively, the DIRECT Algorithm is also able to find global optima and it is faster (when it works);
The genetic method implemented in EES is derived from the public domain Pikaia optimization program (version 1.2, April 2002) written by Paul Charbonneau and Barry Knapp at National Center for Atmospheric Research (NCAR). A detailed explanation of genetic optimization algorithms in general and specific details of the Pikaia program are provided on the Pikaia website. The information available on this website is the best source of information on the theory of the genetic optimization method implemented in EES. The information provided below is not intended to substitute for the Pikaia documentation, but rather to provide the user with necessary information to effectively use this optimization method.
The genetic method intends to mimic the processes occurring in biological evolution. A population of individuals (i.e., sample points) is initially chosen at random from the range specified by the bounds of the independent variables. The individuals in this population are surveyed to determine their fitness (i.e., the values of the objective function as quantified by the value of the variable that is to be minimized or maximized). Then a new generation of individuals is generated in a stochastic manner by 'breeding' selected members of the current population. The characteristics of an individual that are passed on to the next generation are represented by encoded values of its independent variables. The probability that an individual in the current population will be selected for breeding the next generation is an increasing function of its fitness. The 'breeding' combines the characteristics of two parents in a stochastic manner. Additional random variations are introduced by the possibility of 'mutations' for which the offspring may have characteristics that differ markedly from those of the parents. In the current implementation, the number of individuals in the population remains constant for each generation.
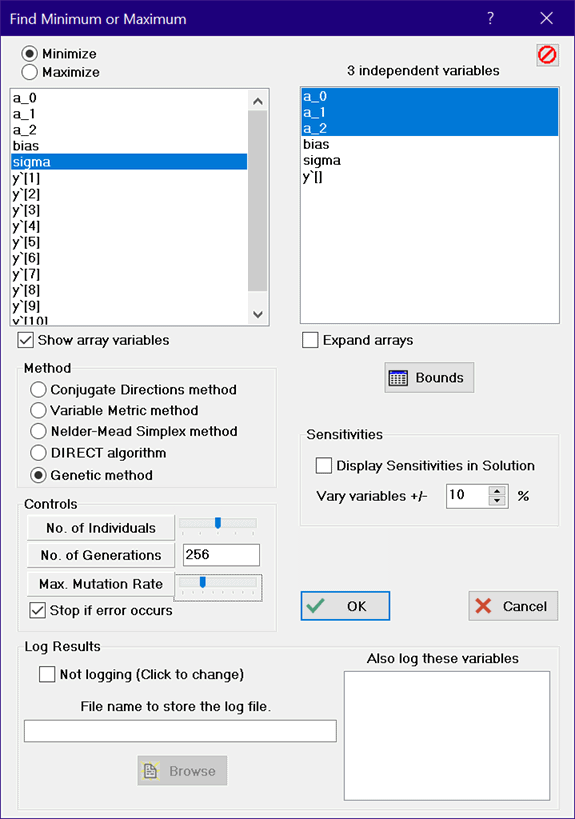
The three parameters in the genetic method that are most responsible for identifying an optimum and for the associated computing effort are the number of individuals in a population, the number of generations to explore, and the maximum mutation rate. These parameters can be specified using slider bar controls. Alternatively, the value of each parameter can be directly specified in the edit box that appears when you click on the button to the left of the slider bar control. The dialog below shows both options.

Using the slider bar controls, the number of individuals can range from 16 (far left) to 128 (far right) and the number of generations can ranges from 16 (far left) to 2048 (far right). For both of these slider controls, each tick results in a factor of two change in the parameter value. The slider bar range for the maximum mutation rate is from 0.0875 (far left) to 0.7(far right) with linear variation. (When using the edit box parameter entry, any positive value can be entered for any of these parameters.) Larger values for the maximum mutation rate cause the algorithm to search more aggressively for an optimum at locations distant from the current optimum. Smaller values focus the search more around the current optimum. There are other parameters in the genetic algorithm (e.g., the minimum mutation rate, the number of significant figures to encode, etc.). These and others have been set to the default values suggested in the Pikaia program and are not changeable within EES.
Clicking the icon at the upper right of the dialog unselects all independent variables.
If the Expand arrays check box is not checked, arrays will be displayed in the Independent Variables list as one item, e.g., y`[]. Clicking on this item will expand the array so that one or more of the array elements can be selected as independent variables.
Unlike the Conjugate Directions and Variable Metric methods, the genetic method is not affected by the guess values of the independent parameters. However, the lower and upper bounds on the independent parameters are extremely important since the initial population and subsequent stochastic selections are chosen from within the bounds. Use care in selecting the bounds.
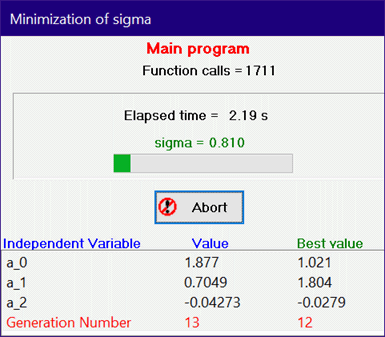
As mentioned previously, the genetic method is robust but slow. The number of function evaluations required is approximately equal to the product of the number of individuals and the number of generations. Setting the slider bar controls for the number of individuals and generations to their rightmost positions will result in more than 262,000 function evaluations. Depending on the complexity of the objective function, the calculations may require just short of forever to complete. The progress of the optimization is displayed during the calculations, as shown below. The best value of the objective function that has been found is displayed in green type below the elapsed time. The values of the independent variables that produced this optimum are shown in the 'Best value' column at the bottom right. The number of generations completed is represented by the progress bar above the Abort button. Should you tire of waiting for the calculations to complete, you can click the Abort button. The Solution window will then display the best point found up to time when the calculations were terminated.
Return to Min/Max.